대부분 알고리즘책의 첫 단원에 Big-O, Big-θ, Big-Ω가 나온다. 처음에 보면 낯설다. 그리고 알고나서 꼭 이렇게 어려운 말로 해야했나라는 생각이 든다. 그럼 왜 Big O라 말할까? 아주 옛날에 Paul Bachmann이라는 사람이 제안했다고 한다. 그냥 받아들이자.
셋 중에 제일 많이 사용되어지는 것은 Big O 이다. 컴퓨터과학에서 알고리즘의 복잡도를 분석하는 가장 근본적인 방법이다. 왜 "Big O notation"이 가장 많이 사용되어지나?
Big O는 내가 시한부 환자가 되서 의사에게 "저 언제까지 살 수 있죠?" 라고 물어봤을때 많은 의사들이 쓰는 방법 같은 것이다. 보통의 의사들이 최악의 경우를 염두해 얘기할 것이다. 즉, 다른 사람들에게 내 알고리즘의 복잡한 정도를 얘기할때 최악의 경우를 염두해두고 말하는 방법이 Big O이다.
우리는 Bio O로 시간복잡도와 공간복잡도를 표현하는데, 대부분 문제에서 더 중요하게 많이 다루는 것이 시간복잡도 이므로 시간복잡도부터 써보기로 한다.
왜 처음에 어려울까? 아래는 대학에서 처음에 알고리즘을 공부할때, 책이나 강의 노트에서 볼수 있는 말이다.
\begin{equation*} \begin{split} O(g(n)) \, is \, a \, set \, of \, all \, functions \, with \,a \,lower \,or \,same \,order \, of \, growth \,as \,g(n) \\ \end{split} \end{equation*}
\begin{equation*} \begin{split} T(n) \quad is \quad O(g(n)) \quad if \quad T(n) \in O(g(n)). \\ \end{split} \end{equation*}
어렵다. 우선 O(g(n)) 부터 뜯어보자. g(n) 자리에 1, log n, n, nlogn, n2, 2n ,n! 등을 쓴다. 그렇다. g(n)의 n의 함수이다. 그런데 O안에 g(n)에는 기본형으로만 표현한다. 만약 1차 함수라고 한다면 'an + b'의 형태가 아니라 그냥 'n'만 쓴다. 왜? 그렇게 약속되었다. 이건 정확한 복잡도, 이거 몇번 반복되? 라고 구체적 숫자를 묻는 약속이 아니다. 사실 컴퓨터한테 위에서 a와 b과 아주 큰 의미있느 숫자가 아니기 때문이다. 물론 저 'a'가 무척 큰 숫자면 어쩌냐고 물어보는 사람도 있는데, 그건 아주 특수한 경우이다.
그리고 상수가 큰 경우는 처음부터 고려해서 프로그램을 짤 것이다. 문제는 처음에는 잘 돌아가다가, 처리할 데이터가 늘어나면서 느려지거나 실행이 불가능한 경우일 것이다. nn 알고리즘도 데이터가 5개 이하로 보장된다고 하면 문제없다. 그리고 BigO의 대상도 아니다. Big O는 n이 클 경우에 대한 정의이기 때문이다. (Big-O notation: For large values of n the running time of g(n) is at most b·g(n))
결국 O(Big O)는 들어오는 입력값에 의해 내 프로그램의 재귀함수나 반복문에 의해서 얼마나 반복되는가를 기본값으로 나타낸다. 약간 더 어렵게 말해서 내 알고리즘의 문제해결시간과 입력함수(g(n))과 관계이다. 제일 쉬운 1과 n으로 예를들면,
def bigO(n):
for i in range(1,10000):
print(n)def bioO(n):
for i in range(1, n):
print(n)def bioO(n):
for i in range(1,n):
for j in range(1,n):
print(n)반복되는 for문이 두개면 O(n2) 이다.
def BigO(n):
i = 1
while i < n:
print('i = ', i, 'n = ',n)
i = i * 2위는 i가 두배씩 증가하므로 log(n)이다.
마지막으로 함정이 있는 문제를 예시를 살펴 보면,
def trickyBigO(n, m):
i = m
while (i > 100):
i = i / 3
k = int(i)
j = 1
for k in range(k, 0, -1):
j = 1
while j < n:
print("Tricky j", j)
j = j * 2위 프로그램의 시간복잡도는 어떻게 될까?(정답은 맨아래)
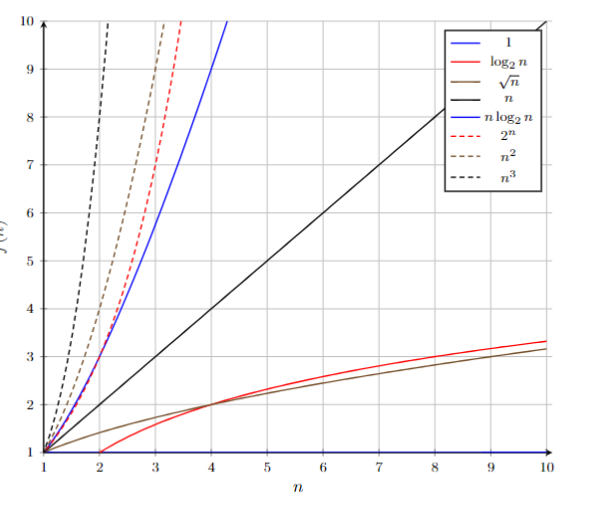
마지막으로 시간복잡도에서의 복잡한 순서와 그래프를 보자.
복잡도 순서:
정답은 $ O(log{}n + log{}m)$ 이다.